سرعت زاویه ای
در این مقاله فرمول سرعت زاویه ای بر روی هر نوع منحنی به اثبات رسیده است
سرعت زاویه ای
در این مقاله فرمول سرعت زاویه ای بر روی هر نوع منحنی به اثبات رسیده است. با توجه به اهمیت محاسبه سرعت زاویه ای در اکثر علوم کاربردی نظیر مکانیک دینامیک ، هوا-فضا، سیستم های دینامیکی و عدم وجود رابطه اثبات شده در این زمینه ، این نیاز احساس میگردد که به منظور طراحی بهینه سازی سیستم های دینامیکی بایستی رابطه ای مستدل ارائه گردد. این مقاله سعی بر آن دارد که رابطه مورد نظر را در ساده ترین حالت ممکن اثبات نماید مقدمه سرعت زاویه ای بر روی هر منحنی : در کتب مکانیک دینامیک تعریف سرعت زاویه ای این طور آمده است : زاویه ای که متحرک در واحد زمان طی می نماید، سرعت زاویه ای می نامند و واحد سرعت زاویه ای عبارت است از رادیان بر ثانیه (Rad/Sec) فرمول سرعت زاویه ای عبارت است از : V=R.ω که در فرمول فوق (V) عبارت است از سرعت خطی بر روی منحنی و (R) شعاع دوران حول محور دوران و (ω) سرعت زاویه ای متحرک. در این مقاله سرعت زاویه ای بر روی هر نوع منحنی را بررسی می نماییم (منحنی بسته و منحنی باز). ابتدا سرعت زاویه ای بر روی منحنی بسته را بررسی می نماییم، در منحنی بسته دو شکل هندسی مشخصه موجود بوده که رایج می باشد. یکی دایره و دیگری بیضی. و در منحنی باز هر نوع منحنی که ابتدا و انتهای آن به یکدیگر متصل نشود را شامل می شود. اینک در آغاز، منحنی بسته را بررسی می نماییم، نخست در دایره سرعت زاویه ای در دایره شامل دو بخش می شود الف: سرعت زاویه ای در دایره با سرعت خطی ثابت نظر به اینکه سرعت خطی (V) در دایره ثابت بوده و شعاع دایره (R) نیز ثابت می باشد لذا سرعت زاویه ای نیز ثابت خواهد بود V=R.ω بنابراین تمام زوایای طی شده در واحدهای زمانی مساوی ω= V/R =cte خواهد بود. ب: سرعت زاویه ای در دایره با سرعت خطی غیر ثابت (متغیر) : نظر به اینکه سرعت خطی (V) در دایره ثابت نمی باشد ولی شعاع دایره (R) ثابت است لذا سرعت زاویه ای غیر ثابت خواهد بود، بنابراین خواهیم داشت :  اینک با توجه به شکل (1) می توان بیان نمود که متحرک از نقطه (A) تا نقطه (B) را در واحد زمان طی نموده یعنی زاویه (α) و از نقطه (B) تا نقطه (C) را در واحد زمان دیگری طی نموده است یعنی زاویه (β). زاویه (α) با زاویه (β) مساوی نخواهد بود. بنابراین می توان نتیجه گرفت که تمام زوایای طی شده در واحدهای زمانی مساوی نخواهد بود یعنی در هر واحد زمانی زاویه ای طی خواهد نمود که بستگی به تغییرات سرعت خطی خواهد داشت. سرعت زاویه ای در بیضی : چنانچه مرکز بیضی را محور دوران در نظر بگیریم و متحرک طوری حرکت نماید که دارای سرعت زاویه ای ثابت باشد می توان فرمول را با توجه به انکه شعاع دوران و سرعت خطی متغیر می باشد بررسی نمود: dV = R * dω + ω.dR = 0 + ω.dR مطابق شکل (2) زوایای طی شده با هم برابر هستند ولی با توجه به شکل می توان نتیجه گرفت که تغییرات سرعت خطی با تغییرات شعاع دوران متناسب است. اینک سرعت زاویه ای را بر روی منحنی باز بررسی می نماییم و فرمول سرعت زاویه ای به اثبات می رسد.
اینک با توجه به شکل (1) می توان بیان نمود که متحرک از نقطه (A) تا نقطه (B) را در واحد زمان طی نموده یعنی زاویه (α) و از نقطه (B) تا نقطه (C) را در واحد زمان دیگری طی نموده است یعنی زاویه (β). زاویه (α) با زاویه (β) مساوی نخواهد بود. بنابراین می توان نتیجه گرفت که تمام زوایای طی شده در واحدهای زمانی مساوی نخواهد بود یعنی در هر واحد زمانی زاویه ای طی خواهد نمود که بستگی به تغییرات سرعت خطی خواهد داشت. سرعت زاویه ای در بیضی : چنانچه مرکز بیضی را محور دوران در نظر بگیریم و متحرک طوری حرکت نماید که دارای سرعت زاویه ای ثابت باشد می توان فرمول را با توجه به انکه شعاع دوران و سرعت خطی متغیر می باشد بررسی نمود: dV = R * dω + ω.dR = 0 + ω.dR مطابق شکل (2) زوایای طی شده با هم برابر هستند ولی با توجه به شکل می توان نتیجه گرفت که تغییرات سرعت خطی با تغییرات شعاع دوران متناسب است. اینک سرعت زاویه ای را بر روی منحنی باز بررسی می نماییم و فرمول سرعت زاویه ای به اثبات می رسد. 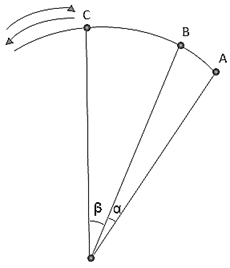
دانلود “سرعت-زاویه-ای1.pdf” سرعت-زاویه-ای1.pdf – 946 بار دانلود شده – 1 MB
